Korelácia je pojem, popisujúci štatistickú závislosť medzi minimálne dvoma parametrami.
Korelácia slúži na stanovenie štatistickej závislosti závislej premennej (tú potrebujeme zistiť) od nezávislej premennej (tú poznáme, alebo ju vieme nastavovať). Korelácia sa väčšinou používa na odhad hodnoty závislej premennej, to znamená predikciu určitého stavu. Je to jednoduchý štatistický model systému.
Korelácia môže byť jednoduchá, vtedy stanovujem súvislosť medzi jednou nezávislou premennou a jednou závislou premennou. Je to najčastejší typ korelácie.
Komplexnejšími sú tzv. viacnásobná korelácia, popisujúca súvislosť jednej závislej premennej od viacerých nezávislých premenných.
Pre koreláciu platia obmedzenia vyplývajúce z jej podstaty. Korelácia popisuje výlučne štatistickú závislosť, nie kauzálnu. Medzi nezávislou a závislou premennou nemusí byť vôbec žiadny priamy vzťah.
Rozdiel medzi kauzálnou a štatistickou závislosťou si môžeme demonštrovať na nasledujúcom príklade:
V New Yorku skúmali viaceré faktory v súvislosti s kriminalitou a zistilo sa, že existuje silný korelačný vzťah medzi počtom predaných zmrzlín a počtom vykradnutých bytov. Ak počet predaných zmrzlín stúpal, stúpal aj počet krádeží. Napriek silnej štatistickej korelácie neexistuje kauzálna príčina medzi predajom zmrzliny a počtom krádeží.
Druhým obmedzením je fakt, že hodnoty závislej premennej je možné predpovedať iba v rámci rozsahu nezávislej premennej, v ktorom sa štatistická závislosť určila. Napríklad, pokiaľ budem merať teplotu vzduchu v závislosti od dennej doby v mesiaci jún, tak môžem odhadnúť teploty vzduchu v určitej hodine iba pre mesiac jún. Pre mesiac január odhad hodnôt nemôžem použiť.
Pretože korelácia určuje tzv. štatistickú závislosť, a nie kauzálnu (príčina-následok) nie je ani pri silnej korelácií možné určiť hodnotu neznámeho parametra so 100% istotou.
Skúmanie korelačnej závislosti je možné vykonať po súčasnom nameraní dostatočného počtu závislej a nezávislej premennej. V druhom kroku sa určuje korelačná závislosť medzi závislou premennou a nezávislou premennou, prípadne premennými. Skúma sa tesnosť korelácie (sila korelácie) a tvar krivky, ktorá reprezentuje závislosť. V najjednoduchšom prípade popisuje vzťah medzi závislou premennou a jednou nezávislou premennou priamka. V tomto prípade vravíme o lineárnej závislosti. Vyjadrením závislosti je rovnica priamky v tvare y = ax+b, kde y je závislá premenná a x je nezávislá premenná.
Na vyjadrenie tesnosti korelácie sa používa korelačný koeficient, ktorý nadobúda hodnoty od -1 po 1. V praxi sa používa jeho druhá mocnina. Ak je korelačný koeficient kladný, medzi premennými je priama úmera. Ak je záporný, medzi premennými je nepriama úmera. Ak je koeficient rovný nule, obe premenné sú štatisticky nezávislé.
Grafickým vyjadrením závislosti je korelačný graf, kde na osi x sú vynesené hodnoty nezávislej premennej a na y osi závislej premennej. Nameranými bodmi je preložená tzv. regresná krivka, ktorá reprezentuje funkciu závislosti premenných. Jej „presnosť“ vyjadruje korelačný koeficient, respektíve jeho druhá mocnina. Čím viac sa hodnota druhej mocniny blíži k 1, tým presnejšie vieme určiť na základe regresnej rovnice hodnotu závislej premennej z hodnoty nezávislej premennej. Pokiaľ je korelačný koeficient rovný 0 (jeho druhá mocnina je potom tiež rovná 0), z hodnoty nezávislej premennej nevieme určiť hodnotu závislej premennej. Závislá premenná sa správa ako náhodná veličina, ktorej hodnotu neovplyvňuje hodnota nezávisle premennej.
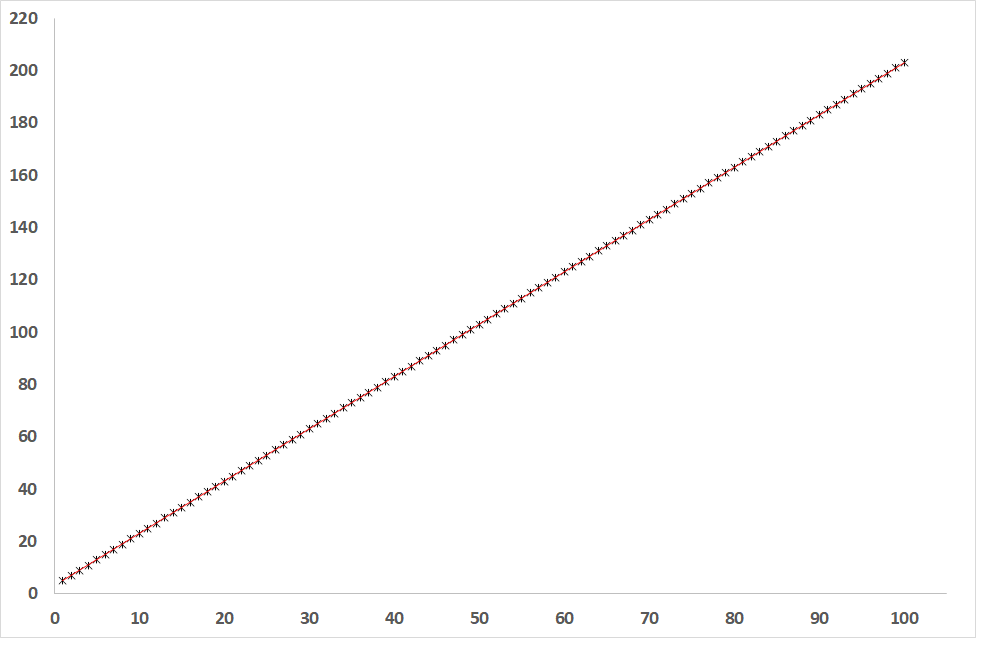
Obr. 1: Závislosť závislej premennej od nezávislej premennej, ak je R = 1 (priamka priamej úmery)
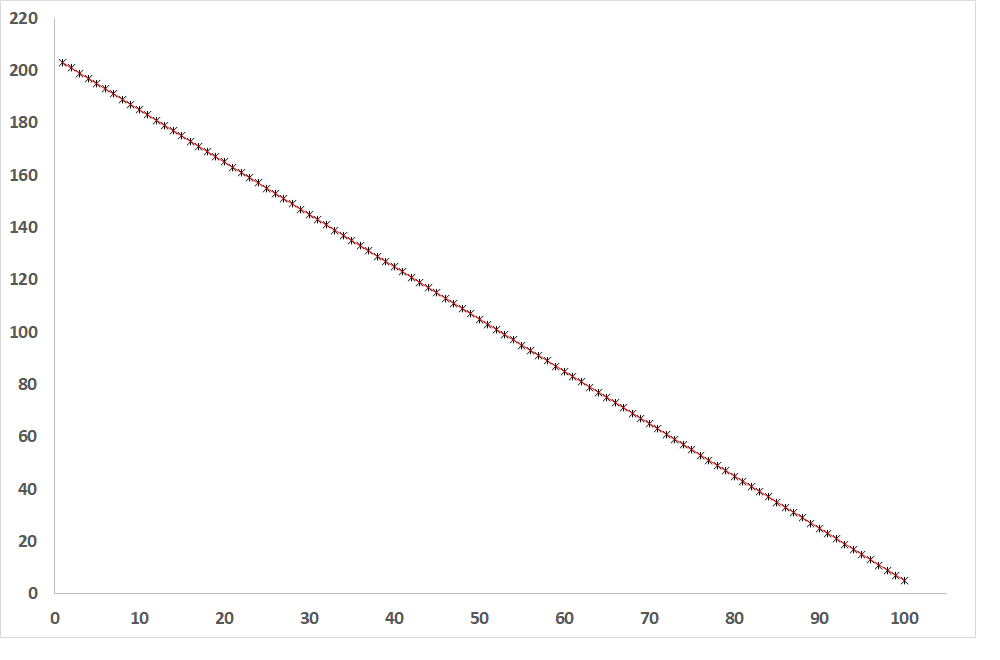
Obr. 2: Závislosť závislej premennej od nezávislej premennej, ak je R = -1 (priamka nepriamej úmery)
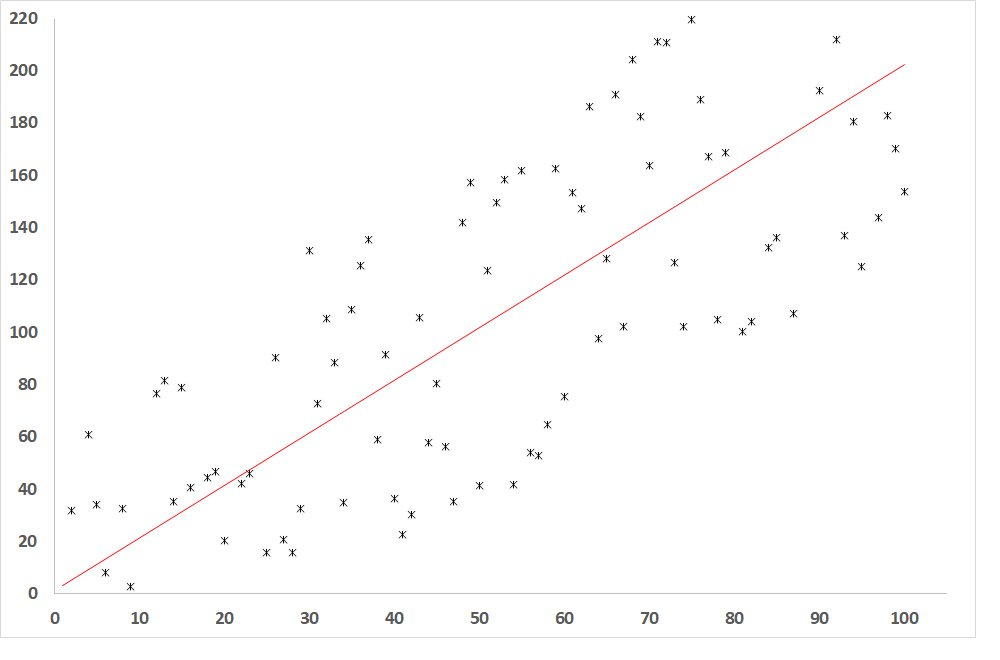
Obr. 3: Závislosť závislej premennej od nezávislej premennej, ak je R = 0,8 (relatívne tesný vzťah medzi premennými)
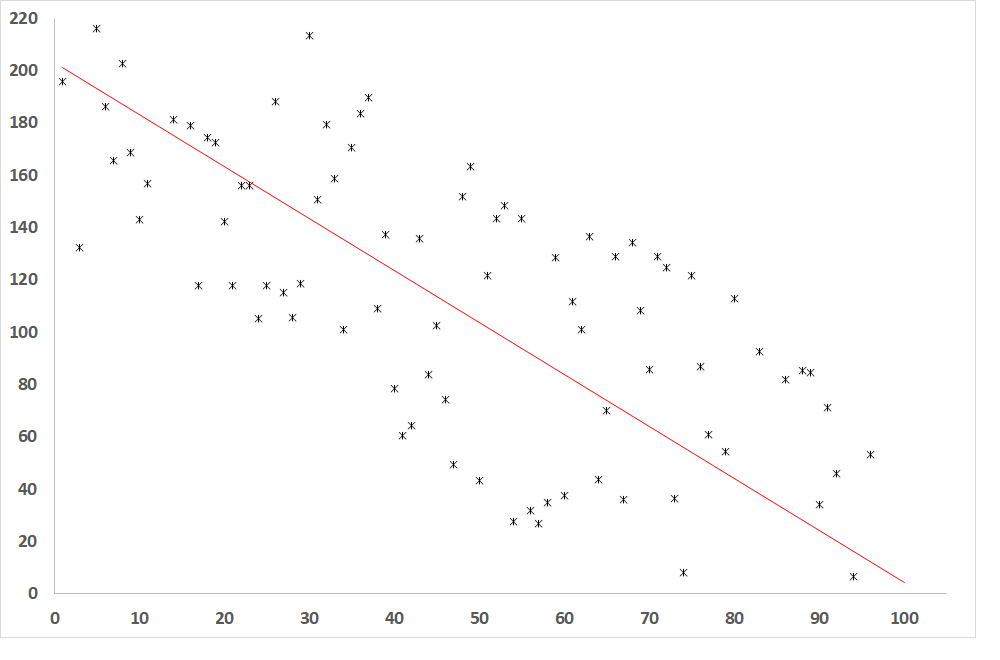
Obr. 4: Závislosť závislej premennej od nezávislej premennej, ak je R = -0,8 (relatívne tesný vzťah medzi premennými)
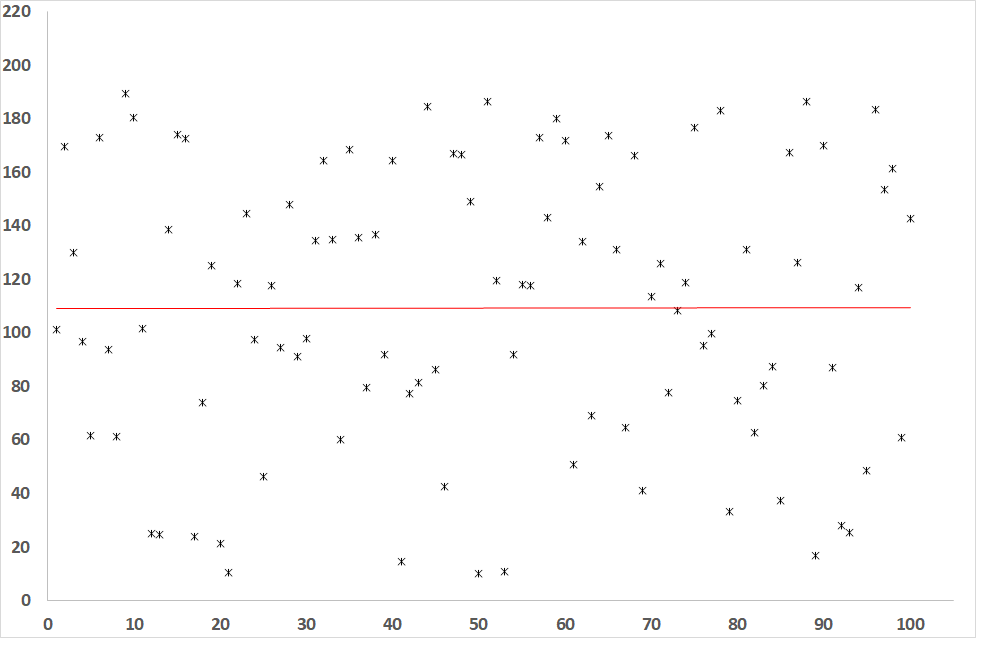
Obr. 5: Závislosť závisle premennej od nezávisle premennej, ak je R = 0 (nie je korelácia medzi premennými)
Problematika korelácie je rozsiahlejšia, tento článok je stručným súhrnom. Pre hlbšie štúdium odporúčame navštíviť niektoré zo školení, ktoré poskytuje naša spoločnosť.
| Názov školenia | Trvanie školenia | Miesto konania | Cena | Najbližší termín |
|---|---|---|---|---|
| Inovatívne metódy využívané v automobilovom priemysle a strojárskej výrobe |
11 dní
(8:00 - 14:00)
|
Online |
1 600,00 €
1 968,00 € s DPH
|
10.06.2025 - 13.06.2025, 17.06.2025 - 20.06.2025, 24.06.2025 - 26.06.2025
+ 3
|
| Základy SPC - Štatistické metódy riadenia procesov |
2 dni
(8:00 - 14:00)
|
Online |
359,00 €
441,57 € s DPH
|
17.06.2025 - 18.06.2025
+ 6
|
| SPC III – Projekt zavádzania štatistických metód v organizácii |
2 dni
|
Firemné školenie | Na vyžiadanie |
Podľa Vás
|
| Six Sigma tréning |
2 dni
|
Firemné školenie | Na vyžiadanie |
Podľa Vás
|
| SPC II – Riešenie problémov SPC |
2 dni
|
Firemné školenie | Na vyžiadanie |
Podľa Vás
|